数学传奇「里奇流之父」逝世，享年81岁！助力证明庞加莱猜想，奠定几何学发展基础

又一位数学巨星陨落！

美国几何分析数学家、哥伦比亚大学戴维斯教授Richard Hamilton（理查德·哈密顿），于9月29日去世，享年81岁。

他一生中，最大的贡献在于引入并发展「里奇流」（Ricci flow）研究。

这是一个用几何分析方法，证明庞加莱猜想的基础。

而且，他还为低维拓扑、微分几何学做出了基础性贡献。

40年来，他进一步深入而系统地发展了这一理论，推动了一个世纪以来几何学领域最基础科学进展。

Hamilton曾在2011年荣获邵逸夫奖，是美国国家科学院院士，也是美国艺术与科学院院士。

几个月前，他还被授予了2024数学基础科学终身成就奖。值得一提的是，颁奖典礼上，还有著名数学家姚期智位列其中。

Hamilton一共发表了46篇研究，其中大部分都与几何流（geometric flows）相关。

1982年，他曾在《Three-manifolds with positive Ricci curvature》论文中，首次引入里奇流的概念，证明了首个长时存在性定理。

论文地址：https://projecteuclid.org/journals/journal-of-differential-geometry/volume-17/issue-2/Three-manifolds-with-positive-Ricci-curvature/10.4310/jdg/1214436922.full

随着时间的推移，学界逐渐认识到了这篇论文的重要性，远远超出了刚刚发表时的认知。

Hamilton开创的里奇流，是一种形变过程，使在复杂空间或曲面中，大范围或全局的不规则性变得光滑。

然而在这个过程中，一些小范围或局部的不规则却可能出现。

这套理论的最大困难，在于弄清楚这些在形变过程中形成的不规则点会如何出现，以及在什么条件下它们不会形成。

在这篇论文开头，Hamilton提出，这项工作的目标是证明以下定理。

假设X是一个紧致三维流形，其黎曼度量具有严格的正里奇曲率。那么，X也具有正里奇曲率的黎曼度量。

在20世纪80年代，Hamilton用它证明了黎曼几何中惊人的新结果。

由此，其对具有正里奇曲率的紧致三维流形进行了完整的拓扑分类。

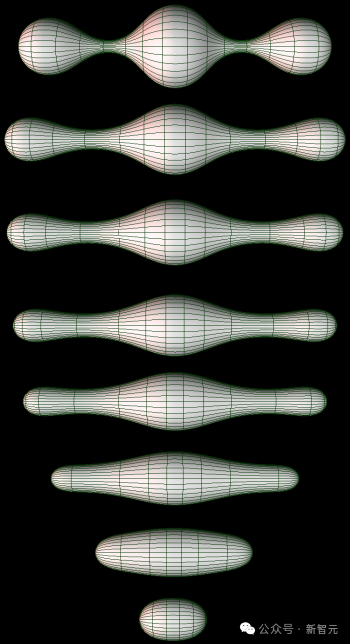
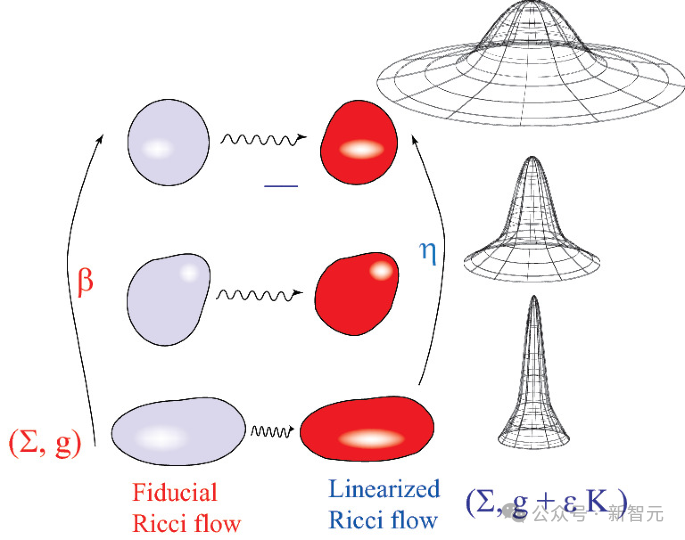
不同时期的里奇流的2D流形

这篇论文一经发表，引发了业界极大的关注。

他提出的里奇流，是一项极富原创性的工作，具有无可比拟的影响力。

当时，Hamilton、丘成桐、Rick Schoen一同被邀请访问UC伯克利数学科学研究所（MSRI）。这是研究所正式对外开放的第一年。陈省身（Shiing-Shen Chern）是研究所的创始主任，Calvin Moore是创始副主任。

第二年，他们三人都加入了加州大学圣地亚哥分校（UCSD），德国数学家Gerhard Huisken也来学校访问。

Hamilton曾在自传中称，有这么多优秀数学家一起研究几何分析中类似问题，进一步推动里奇流的发展。

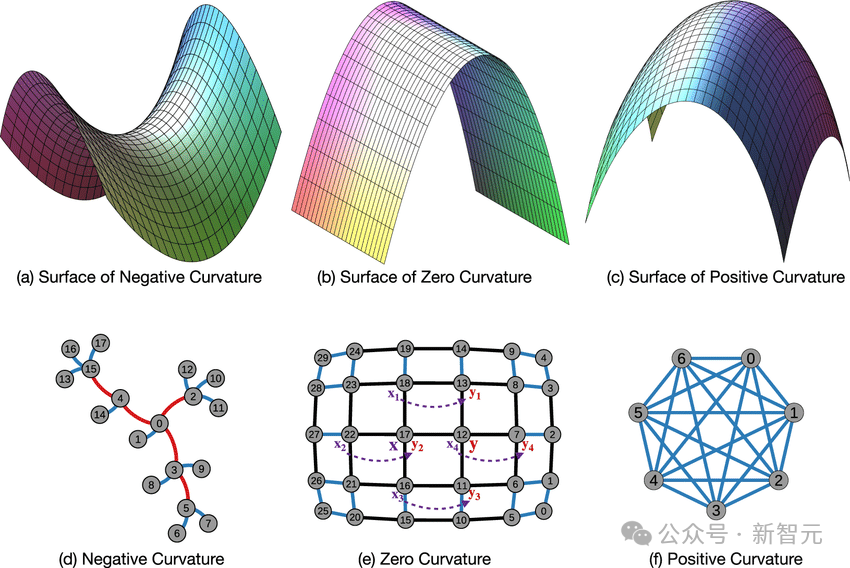
具有负曲率、零曲率和正曲率的流形

丘成桐对此还提出了自己的观点，里奇流可能会在颈部收缩（pinch along necks），这为证明提供了第一步——通过将流行分解，可以维持常曲率几何更简单的部分。

随后，Hamilton从UCSD入职哥伦比亚大学至今。

在此期间，他于1986年将该方法扩展到四维，对具有正曲率算子的紧致四维流形进行分类，推导出重要的李-姚型曲率估计。

这些思想经过发展成为解决黎曼几何、凯勒几何中多个重大问题的工具，包括可微球面定理和在非负双截曲率条件下高秩厄米特对称空间的度量刚性。

随后， Hamilton继续研究三维中的一般里奇流。

他意识到，能否成功地对三维流形进行拓扑分类取决于理解其中可能出现的奇点。并证明了一个基本结果，即当里奇流出现奇点时，曲率为非负。

他还发展了强大的李-丘-Hamilton不等式，以控制里奇流出现奇点时的表现。

随后，Hamilton继续研究三维中的一般里奇流。

1997年，Hamilton发展了带手术的里奇流方法，该方法涉及移除奇点邻域并以可控方式进行替换，使流可以在新获得的流形上继续进行。通过这一流程，对具有正迷向曲率的四维流形进行了分类。

2002年，Grigori Perelman改进了Hamilton的思想，证明了一般三维里奇流的非塌缩定理和典则邻域定理，从而完整的证明了著名的庞加莱猜想。

40年间，他进一步深入而系统地发展了这一理论，推动一个世纪以来几何学领域最基础的学科进展。

2011年，Richard Hamilton获颁有「东方诺贝尔奖」之称的邵逸夫奖，同时难得地披露了自己的早年经历。

流形（manifold）是局部上看起来像欧式空的间拓扑空间，。二维流形被称为曲面（surface）。不会趋向无穷大而是自行闭合的流形称为紧致流形（compact）。

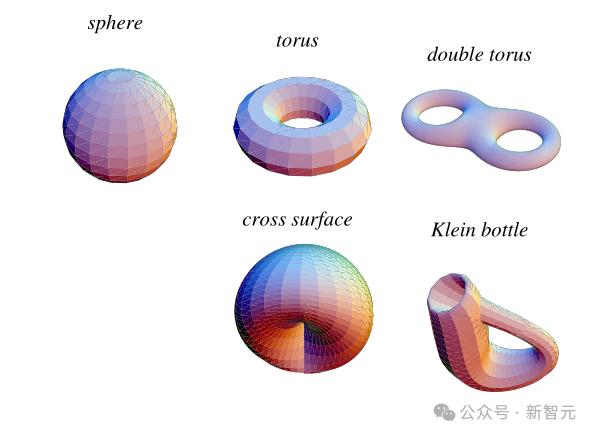
如果不把时间算成一个维度，我们的世界是一个三维空间。但根据爱因斯坦的广义相对论，这个空间不是平坦的而是弯曲的，曲率表现为重力。当然，我们的经验有限，只了解其中的一小部分，因此不知道这个空间的整体形状。就像地球一样，它可能会自行弯曲，或者有虫洞将一个部分连接到另一个遥远的部分。因此拓扑学家自然会问：紧致三维流形（compact three-dimensional manifolds）的所有可能形状都有哪些？

在紧曲面中，球体比较特殊，因为表面上的每条曲线都形成一种包围圆盘的形状；在其他情况下，比如有洞的甜甜圈，围绕孔的曲线则不然。球体这样的流形称为单连通流形（simply connected）。1904年，庞加莱提出猜想，唯一的紧凑单连通三维流形是球体。而Perelman博士在2002年至2003年使用里奇流证明了这一猜想。

流形的度量（metric）是测量点之间的距离。在微分几何中，度量以切向量（tangent vector）的二次函数形式给出，测量其长度的平方。点之间路径的长度由切向量长度的积分给出。

曲面（或流形）上的热方程是一个函数的偏微分演化方程（partial differential evolution equation），其解描述了给定的初始热量如何在曲面（或流形）上扩散，以接近恒定的均匀热量分布。

类似于热方程，里奇流就是流形中度量（metric）的偏微分演化方程，它试图扩展曲率、消除不规则性，以接近恒定的均一分布。庞加莱猜想的思想是，如果度量收敛到恒定的正曲率，则流形必定是球体。